El astrónomo más importante del mundo en su época, los siglos X y XI, era natural de Pedroche. Ishaq Nur ed-Din al-Betrugi o al Bitruyi (Alpetragius para los latinos), astrónomo, filósofo y matemático árabe nació en Pedroche en fecha desconocida, vivió gran parte de su vida en Sevilla y murió en el 1204. En su obra Tratado de Astronomía o Theorica planetarum quiso explicar de forma mecánica el movimiento celeste. Para ello combatió la teoría de los ciclos tolemaicos (ecocéntrico y epiciclo) y se opuso a la teoría según la cual todas las estrellas seguían el movimiento de otra colocada por encima, de la que reciben impulsos procedentes de Oriente y de Occidente, y no en torno a un punto geométrico.
Recurrió a la teoría aristotélica para decir que el sistema astronómico está compuesto por esferas homocéntricas que se organizan en torno a la llamada novena esfera, que constituye el primer motor o “il primum mobile”. Ésta transmite movimiento a otras esferas inferiores en proporción directa a su distancia. También aportó Al-Bitruyi nuevas interpretaciones sobre el orden de los planetas inferiores y sobre el sistema solar. Su obra fue traducida al hebreo en el siglo XIII y al latín por Miguel Escoto en torno al año 1217.
Al Bitruyi no intentó llevar su sistema al grado de perfección al que Tolomeo colocó el suyo y al que no logró desplazar. Tolomeo podía predecir las posiciones de los planetas, algo que el astrónomo nacido en Pedroche ni siquiera intentó.
La obra de Al Bitruyi recibió una calurosa acogida por parte de cuantos se oponían al Almagesto, es especial por los astrónomos árabes, cristianos y judíos españoles, manteniendo su influencia en Italia hasta el siglo XVI.
En su honor se puso su nombre a un cráter lunar, el denominado Alpetragius. Está situado a 16º S y 4,5 O, en el borde oeste del Mar de las Nubes, tiene 44 kilómetros de diámetro y unos 3.900 metros de altura en su contorno. Su cima central está coronada por otros dos microcráteres.
Una muestra de la importancia de la obra de al-Bitruji se recoge en LAS «NOTAS SOBRE AL-BITRŪJI» ATRIBUIDAS A REGIOMONTANUS: SEGUNDAS REFLEXIONES, de MICHAEL H. SHANK, Universidad de Wisconsin-Madison, cuya traducción del inglés es la siguiente:
Hace cuarenta años, Francis Carmody publicó un breve texto astronómico del siglo XV bajo el título «Notas de Regiomontanus sobre la astronomía de al-Bitrûji». Según Carmody, el texto demostraba que el vienés Regiomontanus (1436-76) era crítico con la tradición astronómica homocéntrica (que explicaba los movimientos planetarios mediante esferas concéntricas), y también que había malinterpretado en varios momentos al principal defensor medieval de esa tradición, el astrónomo español del siglo XII al-Bitrūji. Desde Carmody, los eruditos han aceptado la autoría de Regiomontanus de estas notas como firmemente establecida y las han utilizado para evaluar la actitud de Regiomontanus no sólo hacia al-Bitruji sino también hacia los sistemas homocéntricos en general. Con algunas excepciones problemáticas (que se discutirán más adelante), Regiomontanus ha sido considerado como un opositor de la astronomía homocéntrica. Sin embargo, un examen cuidadoso tanto de la transcripción publicada por Carmody como del manuscrito muestra que su atribución de las notas a Regiomontanus es casi con toda seguridad un error.
Se trata de algo más que de un intento pedante de poner en orden el catálogo de los escritos astronómicos de Regiomontano. Una vez que Regiomontanus deja de ser un crítico declarado de al-Bitrüji, su actitud hacia la astronomía homocéntrica se convierte en una cuestión mucho más abierta. A la mayoría de los historiadores de la astronomía les puede resultar difícil creer que un astrónomo matemático sofisticado pudiera tomarse en serio un sistema homocéntrico. Por definición, un sistema de este tipo implica que cada planeta se encuentra siempre a la misma distancia fija de la Tierra, lo que parece contradecir un fenómeno tan conocido como la variación del brillo de Marte, por ejemplo. Y sin embargo, por paradójico que parezca.
Regiomontanus estaba muy interesado en la tradición homocéntrica, a pesar de ser un astrónomo matemático excepcionalmente competente. Al atribuir las «Notas sobre al-Bitrúji» a Regiomontanus, Carmody pensó sin duda que pisaba terreno seguro, pues contaba con el apoyo de Ernst Zinner, el principal biógrafo de Regiomontanus. Curiosamente, ni Zinner ni Carmody han justificado esta atribución. En primer lugar, por lo que sabemos, el texto de las «Notas» sólo existe en un manuscrito (Viena, Österreichische Nationalbibliothek, codex lat. 5203). En segundo lugar, este códice es el famoso «libro de cálculo vienés» de Regiomontanus (el llamado Wiener Rechenbuck), en el que el texto aparece de su puño y letra. Por último, Regiomontanus poseía un ejemplar de la traducción latina del tratado de al-Bitri, De motibus ceforum (actualmente en Nuremberg, Stadtbibliothek Cent. V 53), evidentemente le interesaba este texto y, por tanto, tenía un motivo para comentarlo. Como para confirmar la atribución, Carmody señaló que las «Notas» y la Disputationes contra deliramenta Cremonensia de Regiomontanus compartían un punto de vista similar, «un énfasis exagerado en el Almagesto». Estos argumentos no son muy convincentes. La presunta singularidad de las «Notas» es un artefacto de nuestra ignorancia. Muchos manuscritos de finales de la Edad Media no están suficientemente catalogados, y muchos textos astronómicos en particular siguen esperando a los lectores modernos, por no hablar de atribuciones sólidas. Además, al igual que las «Notas», otros documentos del cuaderno misceláneo de Regiomontanus aparecen tanto de su puño y letra como sin atribución, aunque es evidente que él no los compuso. En resumen, la autoría de las «Notas» por parte de Regiomontano es una suposición. Varios argumentos independientes sugieren que es muy poco plausible.
Si este texto supuestamente único es de Regiomontanus, su copia debe ser un autógrafo autónomo. Sin embargo, tanto el contenido como el aspecto del manuscrito desmienten tal conclusión. Las primeras treinta y tres líneas del texto tienen una unidad de contenido definida: tratan exclusivamente del sistema homocéntrico de al-Bitrüji y de las objeciones del autor al mismo. Las dos últimas líneas, sin embargo, giran en torno a un modelo cosmológico que no guarda ninguna relación con la teoría de al-Bitrüji, como el propio Carmody advirtió. Dado que las «Notas» no están dedicadas únicamente a al-Bitruji, es posible que el texto conservado sea un extracto incompleto de un debate más extenso sobre los sistemas cosmológicos. Esta suposición se ve reforzada por un error notable que cometió Regiomontanus al copiar las tres últimas palabras. Se leen quidem [[contig]] [[sed]] continuos sed contiguor, donde las palabras entre corchetes dobles están tachadas. Si contiguos hubiera sido la última palabra del texto que estaba copiando, sería difícil entender cómo el ojo de Regiomontanus pudo haberse saltado dos veces. Este error es mucho más fácil de explicar si el texto copiado continuaba. De hecho, puede ser significativo que el texto, tal como aparece en ÔNB lat $203, termine en la parte inferior de un folio, en el verso, y al final de una línea. El contenido, la paleografía y la codicología son coherentes con la suposición de que Regiomontanus copió de un texto más largo que el que ha sobrevivido.
Todas las demás tachaduras, errores y correcciones del texto pueden explicarse igualmente como errores de copia. ¿Podría Regiomontanus haber compuesto primero el texto y luego volver a copiarlo él mismo? Ciertamente, esta posibilidad no puede descartarse por completo. Sin embargo, los errores no son del tipo que cabría esperar de un autor que vuelve a copiar su propia obra. Ninguno de ellos tiene que ver con el estilo o el contenido; todos son de carácter puramente caligráfico. De hecho, en la mayoría de los casos, el ojo salta de forma mecánica sin prestar atención al contenido, un comportamiento inusual en un autor que repasa su propia obra. El lenguaje de las «Notas» tampoco tiene el ‘tacto’ de Regiomontanus».
Un examen del contenido revela varios desacuerdos llamativos con puntos de vista que Regiomontanus defendía en otros lugares. El autor del texto defiende una teoría lunar que combina una excéntrica con un epiciclo (véase la línea 19. Apéndices A y B más abajo), una posición también presentada en la Theoria planetarum communis, como señaló el propio Carmody» Pero en las Disputationes de Regiomontano, este mismo modelo hinar es objeto de duras críticas:
El interlocutor de Regiomontanus lo contrapone desfavorablemente a la teoría lunar esbozada en la Theoricae novae planetarum de Georg Peuerbach. Sabemos que Regiomontanus conocía la obra de Peuerbach cuando copió las «Notas»; de hecho, una de las primeras copias conocidas de la Theoricae novae (fechada en 1454) precede a las «Notas» en el libro de cálculos de Regiomontanus (ÖNB lat. 5203, Ir-24r)».
Además, las «Notas» afirman erróneamente que la teoría de al-Bitruji situaba tanto a Mercurio como a Venus por encima del Sol. Carmody tomó este error como prueba de que Regiomontanus había leído De motibus celorum con poca atención. Sin embargo, todas las demás pruebas sugieren que Regiomontanus conocía los puntos de vista genuinos de al-Bitrüjl. En su Epítome del Almagesto, que completó poco después de abandonar Viena, Regiomontanus señaló correctamente que al-Bitruji situaba la esfera del Sol por encima de la esfera de Mercurio y por debajo de la esfera de Venus». Conocía la posición de al-Bitruji de primera mano, ya que poseía un ejemplar del De motibus celorum de este último, supuestamente adquirido durante sus años en Viena. De hecho, en los márgenes de esta copia Regiomontanus no sólo había llamado la atención sobre la inusual posición de al-Bitruji de Mercurio y Venus a ambos lados del Sol, sino que también atribuía a Geber la opinión que el autor de las «Notas» atribuía a al-Bitruji.
Igualmente curioso es que las críticas encontradas en las «Notas sobre al-Bitruj!» no se correlacionan bien con las observaciones marginales autentificadas de Regiomontanus en su copia del De motibus celorum». Al anotar esta obra, Regiomontanus sí criticó a al-Bitrūji, pero no se interesó por las mismas cuestiones que el autor de las «Notas». Así, frente a un pasaje en el que al-Bitruji objeta el movimiento de una excéntrica en un pleno, Regiomontanus escribió: «Impugna la posición de Ptolomeo sin comprender suficientemente los tipos de excéntricas y epiciclos que se utilizan hoy en día en las escuelas».16 La sugerencia aquí parece ser que una comprensión actualizada de estos dispositivos (tal vez en la línea de la Theoricae novae de Peuerbach) no presenta los problemas que al-Bitruji había planteado.
En cada uno de los casos anteriores, las «Notas sobre al-Bitrüji» respaldan posturas a las que se sabe que Regiomontanus se opuso en otros escritos. Si hubiera argumentos independientes para la autoría de las «Notas» por parte de Regiomontano, el texto constituiría la única prueba de que alguna vez sostuvo tales opiniones. Sin embargo, en ausencia de argumentos independientes de su autoría, parece muy arriesgado atribuir estas opiniones a Regiomontano.
Pero hay más. En las «Notas» un intrigante argumento contra el homocentrismo en general se refiere al eclipse solar del 17 de junio de 1433, que el autor describe de la siguiente manera: «…a veces simplemente se eclipsa todo el Sol, pero a veces no todo él, sino su parte media o central, de tal manera que nos aparece iluminado un borde circular redondo, como sucedió en 1433 d.C.» (línea 25, Apéndice B más abajo).
Este pasaje llama la atención por varias razones. En primer lugar, esta descripción clásica de lo que hoy llamamos un eclipse anular es la única ocasión en la que el autor utiliza una observación específica contra el sistema homocéntrico de al-Bitruji. En segundo lugar, es un raro caso en el que el autor entra en el texto en primera persona («se nos aparece…»). Por último, cabe destacar que tanto la fecha del eclipse como la primera persona son superfluas para el argumento, ya que los eclipses anulares en general refutan un esquema planetario homocéntrico.
Esto es cierto: Regiomontano no vio el eclipse de 1433. Nacido en 1436, no tenía ninguna buena razón para referirse en primera persona a esta observación de segunda mano específica. El pasaje tiene mucho más sentido cuando se interpreta como una observación de primera mano reportada poco después del evento por alguien que estaba impresionado por él. Como sabemos por el Epítome, Regiomontano discrepó con la afirmación de Ptolomeo de que el diámetro aparente del Sol era para todos los propósitos prácticos una constante, igual al diámetro de la Luna en el apogeo. Pero el argumento y los datos que utilizó allí para hacer su caso derivan de al-Battani: no hay rastro del eclipse de 1433, que el autor de las «Notas» consideró tan significativo.
A diferencia de Regiomontano, varios otros astrónomos tuvieron un motivo y una oportunidad para observar este eclipse solar específico. En la década de 1430, John de Gmunden estaba en la cima de su carrera en la Universidad de Viena. En agosto de 1432 había predicho un eclipse total del Sol para Viena el 17 de junio de 1433, y utilizó esta información contra las predicciones del juicio final del cartujo Jacob de Clusa. 18 Juan de Gmunden también anunció el próximo eclipse en una nota probablemente dirigida a Georg Müstinger, un ávido astrónomo que también era anterior a Klosterneuburg cerca de Viena.»Gmunden también tuvo varios estudiantes: Georg Prunner copió varias de las obras de Gmunden a finales de la década de 1430 y tenía fama de ser un excelente observador. Otras partes interesadas pueden haber incluido George Müller (o Mülner) de Waldsee (d. 1442), que dio conferencias sobre el Theorica planetarum tres veces durante la década de 1430. Dado su interés constante en la astronomía, él también puede haber oído hablar de la predicción de Gmunden y por lo tanto trató de observar el eclipse.2 En resumen, había cerca de Viena varios astrónomos que estaban en condiciones de saber sobre la predicción de Gmunden de un eclipse total, y de sorprenderse cuando vieron algo que no esperaban luz alrededor de la Luna.
El autor de las «Notas sobre al-Bitrüji» perteneció probablemente al círculo de Viena-Klosterneuburg. Uno de los manuscritos copiados en la esfera de influencia de Müstinger contiene un interesante texto que guarda un estrecho paralelismo con las «Notas» en varios puntos. Se trata de la primera parte de un tratado sobre un instrumento llamado «planitorbium», escrito por un tal «G. Marcho» o «Marchio», a quien el colofón identifica como franciscano de la provincia de Aquitania». Había estudiado en París y estaba en activo a principios del siglo XIV: el prólogo afirma que escribió el tratado en 1310, y más adelante alude a la observación de un eclipse anular en 1309 [1310]. Lo he identificado provisionalmente como el franciscano Guy de la Marche (Guido de Marchia) y utilizaré este nombre en lugar de «Marcho» a continuación.
Las «Notas sobre al-Bitruji» se parecen mucho al texto de Marchia. Varios argumentos de las «Notas» parafrasean de cerca los de Marchia; a veces, las frases son idénticas». Además, Marchia esboza varias disposiciones posibles de Mercurio y Venus con respecto al Sol. Uno de estos esquemas atribuye a los caldeos y egipcios la opinión de que Mercurio y Venus estaban por encima del Sol. Las «Notas» hacen lo mismo, pero dan un paso más al identificar este punto de vista con el de al-Bitrüji. Dado que en el tratado de Marchia, el llamado punto de vista caldeo-egipcio sigue inmediatamente a las críticas a al-Bitruji, un lector apresurado que no estuviera ya familiarizado con los escritos de este último podría fácilmente alejarse del texto con la impresión errónea de que Marchia había identificado la posición caldeo-egipcia con la de al-Bitruji.
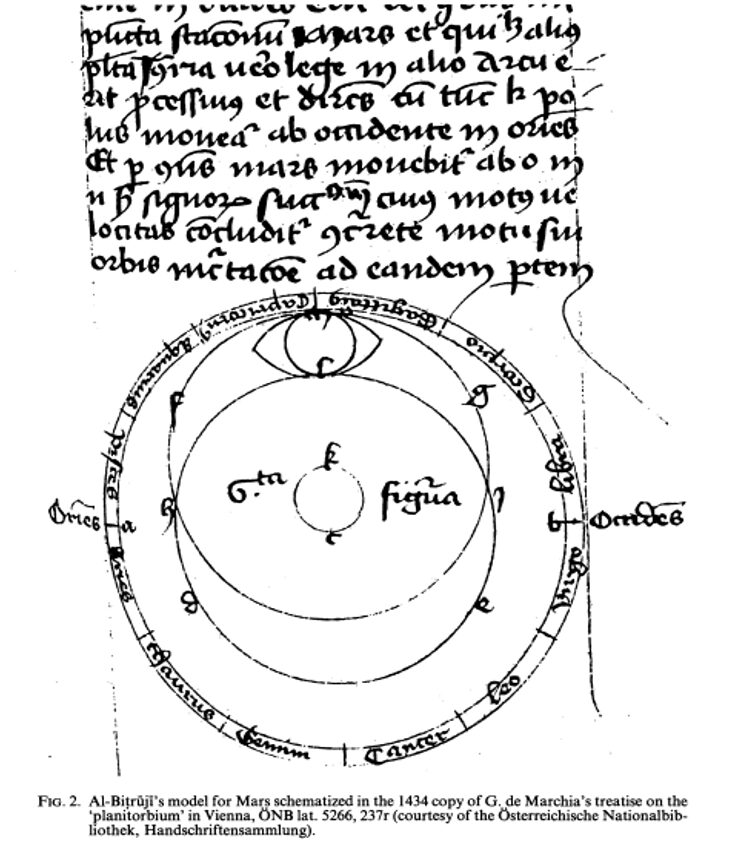
Hay motivos aún más convincentes para postular que el texto de Marchia está detrás de las «Notas sobre al-Bitrüji». En su tratado, Marchia no sólo menciona la ocurrencia de un eclipse anular como argumento contra un sistema homocéntrico, sino que también cita como prueba su avistamiento del eclipse del 31 de enero de 1309 [-1310]. Las «Notas» utilizan el mismo argumento, de nuevo con una redacción muy similar, pero ahora el avistamiento se actualiza a 1433. Es significativo que sólo se conozcan dos ejemplares completos del tratado de Marchia sobre el «planitorbium», y ambos se encuentran en Viena. Como indica el colofón de la copia más antigua (ÖNB, cod. lat. 5266), el escriba escribía en 1434, en Klosterneuburg, a la sombra de Georg Müstinger.
Además, el único diagrama de las «Notas» (figura 1) comparte una notable similitud con la «figura 6» del texto de Marchia (véase la figura 2), que pretende dar el modelo de Marte de al- Bitruji. Gran parte de la letra es idéntica: AB para la eclíptica, CK para el epiciclo polar, DE para el círculo en torno a C, LM para la contrapartida de CK en la eclíptica sorprendentemente dibujada a la vez como un círculo y como un óvalo (Marchia utiliza explícitamente la palabra «ovalis» en el texto).
Por último, el curioso sistema esbozado en las líneas finales de las «Notas sobre al-Bitrüji», atribuido a un quidam alius, se asemeja mucho a la cosmología esbozada en el texto de Marchia: un sistema en el que los planetas no se encuentran en esferas, sino en «círculos columnares», o tores, que se mueven en un medio fluido. Las pruebas anteriores sugieren la siguiente hipótesis: que un astrónomo (aún no identificado) de la época del círculo de Gmunden-Müstinger compuso una crítica de al- Bitruji que se basó en gran medida en el material parisino de Marchia de principios del siglo XIV, y actualizó adecuadamente la observación parisina del eclipse anular de enero de 1310 con la reciente observación vienesa de 1433″. Con toda probabilidad, fue esta versión intermedia la que Regiomontanus copió en su propio cuaderno para su posterior consulta, presumiblemente en una época en la que él también estaba recopilando información sobre al-Bitrûji y sobre otras cosmologías alternativas. Por sí solos, ninguno de los argumentos mencionados contra la autoría de las «Notas» por parte de Regiomontano es decisivo. Sin embargo, en conjunto y en el contexto de la debilidad de los argumentos a favor de su autoría, estos argumentos hacen que sea muy improbable que Regiomontano compusiera este texto. Si las «Notas sobre al-Bitrüji» no son de Regiomontanus, su actitud hacia la astronomía homocéntrica merece un serio reexamen. Siguiendo a Zinner, Helmuth Grössing ha señalado un pasaje de la correspondencia de Regiomontanus con Giovanni Bianchini, que sugiere simpatía por el homocentrismo. Más recientemente, Armin Gerl ha comentado el mismo pasaje y ha vuelto a llamar la atención en prensa sobre una carta de Regiomontanus a Johann Vitéz (1460), que Zinner descubrió a principios de los años cincuenta. En esta carta, Regiomontanus declara su intención de escribir una obra en cuatro partes en apoyo de la astronomía homocéntrica, para lo cual procedió a esbozar teorías sobre el Sol y la Luna en la carta:

También completaré una nueva obra en cuatro tratados, en el primero de los cuales destruiré la antigua teoría de las excéntricas y los epiciclos mediante sólidas razones y observaciones futuras. En el segundo expondré claramente una teoría de los orbes concéntricos por la que se pueden salvar todas las desigualdades de los movimientos. En el tercero confirmaré con pruebas geométricas lo expuesto en el segundo. El cuarto contendrá la manera en que los movimientos pueden ser cuantificados, y las tablas pueden ser establecidas de acuerdo con estas nuevas posiciones en la época.
Viniendo como vienen del coautor del Epítome del Almagesto, estas palabras son desconcertantes. Es evidente que Regiomontanus nunca escribió el tratado que prometió; sin embargo, su intención de hacerlo abre una serie de nuevos problemas sobre su evolución como cosmólogo desde sus años vieneses hasta la década de 1460. Si las «Notas sobre al-Bitruji» ya no representan los puntos de vista de Regiomontanus, la «Carta a Vitéz» puede salir de las sombras para recibir atención por derecho propio. Como mínimo, parece que el desarrollo intelectual del joven Regiomontanus incluyó una fase homocéntrica distintiva. Sus escritos merecen ser reevaluados a esta luz, con especial atención a la longevidad de su perspectiva homocéntrica, su posible impacto en sus cuestiones de investigación y sus actitudes críticas, su relación tanto con sus predecesores en la Universidad de Viena como con sus conocidos en Italia, sus vínculos con las diversas tradiciones filosóficas naturales de su época y su lugar en la evolución de sus puntos de vista cosmológicos.
APÉNDICE B: Traducción
<Refutación de los errores de la obra de al-Bitruji sobre los movimientos celestes>
<1> Al-Bitruji pensaba que todos los orbes celestes se mueven de este a oeste, pero que los orbes inferiores se quedan cortos en la revolución completa del firmamento en un día. Llamó a este déficit el movimiento de «quedarse corto» y <dijo> que de esto resulta que los orbes inferiores parecen moverse opuestamente al primer movimiento, mientras que en realidad todos los movimientos celestes son de este a oeste. <2> Porque él pensaba que sólo una inteligencia es la que mueve todos los orbes, muy cerca del primum mobile, que [la inteligencia] a causa de su cercanía tendría una mayor influencia en el movimiento entre las esferas cercanas, y una menor en las esferas más distantes. Por lo tanto, a causa del desfase, las esferas superiores se alejarían muy lentamente de una revolución completa; las inferiores, en cambio, más rápidamente. <3> Así Saturno se quedaría corto del número de revoluciones diarias del primum mobile en un circuito en 30 años; Júpiter en 12; Marte en 2; el Sol, Venus y Mercurio en uno; la Luna una vez al mes.
<4> De esta manera quería que la oposición y la multiplicidad en los movimientos celestes se eliminaran si se podía mantener una similitud en los movimientos en la misma dirección. A continuación, siguiendo la noción del Comentador <Averroes> en Metafísica XII, con la que intentaba destruir las excéntricas y los epiciclos, supone que todos los orbes celestes son concéntricos, creyendo <podrá> salvar con tal suposición las aparentes irregularidades individuales entre los cuerpos celestes. <5> Pues dijo que los planetas se mueven en sus orbes alrededor de los polos del Zodíaco y, al mismo tiempo, que los polos de sus orbes se mueven en las circunferencias de dos pequeños círculos que pasan por los polos del Zodíaco. <6> Por ejemplo: sea AB la eclíptica, Cits el polo norte, DE el círculo del orbe concéntrico del planeta en el plano de la eclíptica, cuyo polo es igualmente C. Sea entonces CK uno de los pequeños círculos que el polo del orbe planetario describe al pasar por encima» del polo C; <7> y así cuando el polo del planeta está en C, el planeta está en el plano de la eclíptica (como en L) y todo el círculo <=círculo LDE> del orbe planetario <está> igualmente en el plano de la eclíptica. <8> Pero cuando se aleja de C la mitad de la <circunferencia del > pequeño círculo (como cuando está en K), entonces el plano del círculo del orbe planetario <=círculo MDE> debe necesariamente intersecar el plano de la eclíptica y ser intersecado por él a lo largo del diámetro del mundo, de modo que una mitad de él se inclina hacia el sur, la otra hacia el norte en la misma medida <Figuras 1, 3>.
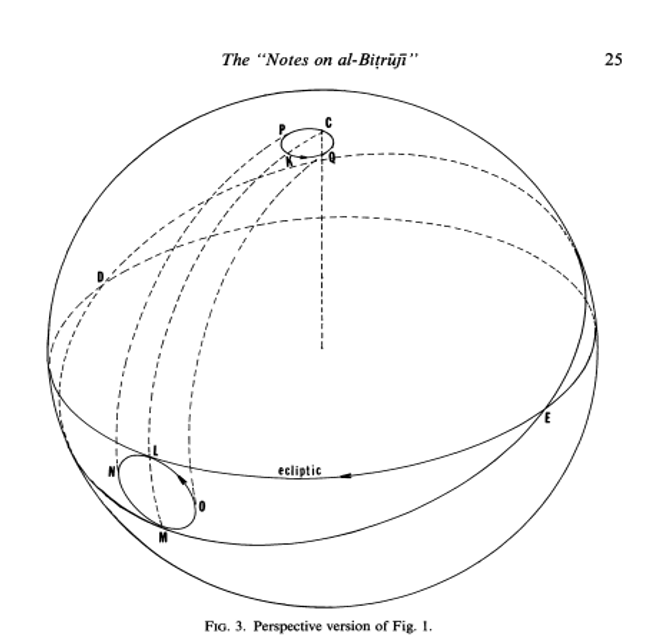
<9> Y si el planeta está entonces en el gran círculo que pasa por ambos polos (es decir, los polos del planeta y del Zodíaco), debe estar en su mayor latitud desde la eclíptica, como en el punto M. Cuando, sin embargo, el polo se mueve de K hacia Q, entonces el planeta parece moverse de M hacia O, por lo que entonces aparece retrógrado. <10> Así, cuando el polo se mueve a través de la mitad PKQ del círculo, el planeta parece estar estacionario, o lento y retrógrado, porque su trayectoria es entonces a través de NMO, pero cuando el polo se mueve a través de la mitad QCP, entonces por el contrario el planeta parece estar en movimiento directo, y moverse a través de OLN, con esta (cualificación] que la concéntrica del orbe planetario se acorta de oeste a este en el orden de los signos. <11> Y así también dijo <que> cuando el polo se mueve en una mitad de su pequeño círculo (tal como QCP) en el orden de los signos y también su caída corta estaría en el orden <de los signos>, su movimiento se aceleraría. <12> Cuando, sin embargo, el polo se mueve en la otra mitad (como PKQ) en contra del orden <de los signos>, entonces se produciría una ralentización, detención o retrogradación del movimiento, según <el movimiento> correspondiera más, o menos, o igualmente al acortamiento del movimiento según la sucesión, habiéndose recorrido así el arco en contra de la sucesión de los signos.
<13> También quiso que el movimiento del orbe planetario en la dirección del movimiento del firmamento fuera alrededor del polo K y no alrededor de los polos del Zodíaco, de tal manera que siguiera el movimiento del firmamento alrededor de los propios polos de su orbe. Estos polos serían inmóviles con respecto al movimiento por el que el orbe sigue al firmamento; móviles, sin embargo, al describir sus circunferencias cerca de los polos del Zodíaco.
<14> Pero está claro que esta suposición de al-Bitruji no se sostiene. En primer lugar, si no hubiera ninguna desigualdad en los movimientos de los planetas aparte del movimiento de quedarse cortos (como él parece querer), entonces Venus y Mercurio en ciertos momentos deberían estar opuestos al Sol, lo que va en contra de la experiencia. <15> Del mismo modo, si la caída corta fuera proporcional a la distancia del firmamento, entonces Mercurio debería caer más corto que Venus, y por lo tanto a veces debería estar enfrente de Venus. <16> Asimismo, si <el punto> relativo al movimiento de los polos de los orbes fuera cierto, entonces el movimiento directo y la retrogradación serían necesariamente más rápidos cuando los planetas están en su máxima latitud y en caso contrario no, lo cual es muy falso. <17> Igualmente, parece que los arcos de movimiento directo o retrogradación serían iguales en todas partes del Zodíaco, pero creo que no es así.
<18> Asimismo no todas las apariencias pueden salvarse de este modo, primero porque, cuando la Luna está en la misma relación con el cenit en diversos momentos y el aire está en un estado de pureza comparable, <la Luna> tiene paralajes diferentes, mayores en un momento, menores en otro, lo que no puede ser el caso a menos que se acerque o se aleje más del centro del mundo. <19> Asimismo, dado también que la Luna está en la misma relación en su anomalía verdadera, o en su centro <=anomalía excéntrica> o elongación desde el Sol, y dado que lo anterior sigue siendo válido, sigue teniendo un paralaje mayor en un momento que en otro, lo cual no puede salvarse con una excéntrica sola, o un epiciclo solo, sino que requiere que se asuman ambos. <20> Asimismo cuando <la Luna> en varios eclipses parciales tiene una latitud totalmente similar, la parte eclipsada también aparece a veces bajo una porción de un círculo mayor, a veces bajo una porción de uno menor; lo cual no puede ser el caso a menos que entre a veces en una sombra más gruesa, a veces en una más pequeña, dado también que el Sol se encuentra entonces a una distancia comparable del apogeo de su excéntrica. <21> Del mismo modo, cuando la Luna en varios eclipses totales tiene una latitud comparable, cuando tiene también la misma velocidad en movimiento, un eclipse también dura más que otro, lo que de nuevo no puede ocurrir a menos que sea debido a un mayor o menor tránsito en la sombra. <22> También los tres <planetas> superiores, cuando están opuestos al Sol, se ven siempre bajo un ángulo mayor que cuando están en cuadratura o más cerca del Sol; lo que sin embargo nunca aparece entre las demás estrellas que están fijas, cuya causa no puede ser otra que una mayor y menor distancia de nuestros ojos. <23> Asimismo cuando están en oposición al Sol, nunca se da el caso de que aparezcan bajo los mismos ángulos, lo que no sólo argumenta que hay epiciclos, sino excéntricas además; y esto es más evidente en Marte. <24> Igualmente cuando Venus y Mercurio están en su salida vespertina, aparecen mucho más pequeños en tamaño; cuando están en su puesta vespertina, sin embargo, mucho más grandes cuando se acercan al Sol en forma retrógrada, dado también que sus elongaciones desde el Sol en ambos casos son iguales. Lo mismo ocurre con la salida y la puesta de la mañana. Además, aunque se adopten anomalías iguales o centros verdaderos, también aparece una desigualdad, lo que argumenta no sólo a favor de los epiciclos, sino también de las excéntricas con epiciclos.
<25> Igualmente en los eclipses solares, cuando la latitud aparente de la Luna es cero, a veces simplemente se eclipsa todo el Sol, pero a veces no todo él, sino sólo> su parte media o central, de tal manera que nos aparece iluminado un borde circular redondo, como ocurrió en 1433 d.C. <26> De nuevo, cuando la Luna es vista en una latitud similar en varios eclipses, la cantidad eclipsada parece diferente; también la duración de los eclipses parece diferente, lo que no puede ser sino por diferencias en la elongación y distancia de las luminarias entre sí y de nosotros. <27> Del mismo modo, cuando el aire no interfiere, el Sol siempre parece más grande cuando está cerca del comienzo de Capricornio que cuando está en el lado opuesto del Zodíaco. <28> Del mismo modo, es razonable que los planetas se muevan más lejos y más cerca de nosotros; de hecho, ya que son esféricos, cuanto más lejos están de nosotros, más partes de sus cuerpos exponen a nosotros, por lo que más influencia ejercen. Por eso se dice que son más fuertes en los apogeos de sus círculos. Pues cuanto más alejada está una esfera luminosa mayor de otra menor, más numerosos son los rayos que pueden alcanzar a la menor.
de <29> A continuación, siguiendo la opinión de los antiguos caldeos y egipcios, al-Bitrûji situó a Venus y Mercurio por encima del Sol. Que esto no es así, sin embargo, queda claro por el paralaje, que es mayor en Mercurio que en Venus; también mayor en Venus que en el Sol, dado que tienen una relación similar con el cenit y el horizonte. <30> Asimismo, siendo el Sol la fuente de calor y luz, debe estar en medio de los planetas, como un rey en su reino, como el corazón en un animal. Y de ello no se sigue que, si están por debajo del Sol, deban completar siempre un circuito del Zodíaco más rápido que el Sol. Porque es cierto que a veces lo hacen más rápido, a veces más lento según como sus centros se ajusten a las anomalías. <31> Tampoco se deduce de esto que, por lo tanto, deban eclipsar a veces al Sol, pues el Sol es tan grande que, aunque fuera eclipsado por Venus o Mercurio, nadie lo percibiría. <32> Dado también que los cuerpos de los planetas distintos de la Luna no absorben más luz solar que la Luna, sino que debido a las variaciones en la porosidad de los planetas y las estrellas, los planetas distintos de la Luna reciben rayos solares en su profundidad. La Luna, sin embargo, debido a su mayor densidad, no es iluminada hasta su centro, de donde nos aparece como una astilla. <33> Pero Venus, por muy cerca que esté del Sol, nunca aparece así como una astilla, ya que la luz solar penetra completamente en su cuerpo. Así pues, es evidente que la opinión de al-Bitruji no basta para salvar los fenómenos relativos a los movimientos de los cuerpos celestes. <34> Hubo otro que afirmó que el cuerpo celeste es todo un continuo, pero en él no hay orbes, sino círculos columnares o figuras redondeadas, y en ellos fijó los epiciclos. Pero esto ciertamente no puede valer para Venus y Mercurio, cuyos deferentes se desvían a un lado y a otro; ni tampoco puede salvarse su movimiento en latitud. <35> Igualmente esto no salvará el movimiento de acceso y receso de la octava esfera, a no ser que se coloquen sobre ella dos orbes que no sean continuos sino contiguos. (*)
Los descubrimiento de al-Bitruji también son recogidos en otras obras como:
Çimen, Ü. (2019). On Saving the Astronomical Phenomena: Physical Realism in Struggle with Mathematical Realism in Francis Bacon, Al-Bitruji, and Averroes. HOPOS: The Journal of the International Society for the History of Philosophy of Science, 9(1), 135-151.
Avi-Yonah, R. S. (1985). Ptolemy vs al-Bitruji: A Study of Scientific Decision-Making in the Middle Ages. Archives internationales d’histoire des sciences, 35(114-115), 124-147.
Goldstein, B. R. (1971). Al-Bitruji: On the principles of astronomy. An edition of the Arabic and Hebrew versions with translation, analysis and an Arabic-Hebrew-English glossary. Al-Bitruji: On the principles of astronomy. An edition of the Arabic and Hebrew versions with translation.
Sabra, A. I. (1984). The Andalusian revolt against Ptolemaic astronomy: Averroes and al-Bitruji. Transformation and Tradition in the Sciences, 133-53.
al-Bitruji Nur al-Din, & Goldstein, B. R. (1971). Al-Bitruji on the Principles of Astronomy. Yale University Press.
Hermeunk, H. (1974). Al-Biṭrūjī: On the Principles of Astronomy.
(*) Traducción del inglés: Francisco Javier Sicilia Romero.
Francisco Sicilia Regalón
Cronista oficial de Pedroche

